A matematikafilozófia története
A matematikafilozófia története azokat az eseményeket, elméleteket öleli fel, melyek a matematikáról mint tudományról való gondolkodással kapcsolatosak. A matematikafilozófia története nem a matematika története, hanem alapvetően a matematika tudományfilozófiájának, a matematikában felmerülő filozófiai kérdéseknek a története. Vannak olyan matematikatörténeti események, melyek nem játszanak fontos szerepet ebben a tekintetben és természetesen a fordított helyzet is előfordul. A szócikk alapvető kérdése az, hogy vajon a különböző korokban hogyan vélekedtek a matematikáról, milyen kép élt erről a tudományról művelői, a matematikusok elméjében.
Az ókor matematikafilozófiája
A folyammenti kultúrák matematikaképe
A korai civilizációk matematikai megállapításai elsősorban a technika feljődésének velejárójaként, mint tapasztalati törvények jelentek meg. Az építészet történetének homályába vész a derékszög-szerkesztés azon módjának eredete, hogy 3, 4 és 5 egység hosszúságú köteleket kell kifeszíteni háromszög alakban, eképp az 5 hosszúságú kötéllel szemközti szög derékszög. A kör kerületének az átmérőjéhez való viszonyszámára közelítő törteket írtak fel, melyek egyik generációról a másikra hagyományozódtak.
Egyiptomban a szögletes testek térfogatának kiszámítását egyfajta átlagszámítással végezték el. Mind Egyiptomban, mind Mezopotámiában számítási eljárásokat dolgoztak ki a kevésbé egyszerűbb törtmennyiségekkel végzett számítások és a magasabbrendű műveletek megkönnyítésére.
Az elméleti jellegű kérdések inkább szöveges feladatokban megfogalmazott első és másodfokú egyenletek megoldására vonatkoztak, melyekben sikereket értek el, bár általános módszerük nem volt az összes gyök megkeresésére.
A matematikai tárgyú történeti forrásokból arra következtethetünk, hogy az ősi kultúrák a matematikában nem törekedtek valamiféle teljes, vagy pontos megoldás megadására. Ez annak köszönhető, hogy a matematikára elsősorban mint alkalmazott tudományra tekintettek, melynek feladata a közgazdasági, építészeti, csillagászati (ill. tengerhajózási) számítások elvégzésének megkönnyítése volt. A teljes pontosság helyett az elég jó közelítés volt a céljuk, de semmiképpen sem egy esetleges megoldás teljeskörű elméleti vizsgálata, körülbelül úgy, mint a mai numerikus matematika esetén. Ezt látszik alátámasztani az is, hogy az ezzel a hagyománnyal közvetlen kapcsolatban lévő indiai matematika például az arkusztangens függvény értékeit már a 14. században végtelen sor segítségével volt képes kiszámítani (bizonyos tekintetben érvényes gondolatmenettel, noha jellemző módon a mai értelemben vett bizonyítás nélkül).
Thalész és a korai püthagoreusok (Kr.e. VII–VI. sz.)
A görög matematika, szemben az egyiptomival és a babilonival, elrugaszkodva az építészeti és közgazdaságtudományi alkalmazásoktól, önálló tudománnyá fejlődött. A görög matematika első időszakában a geometria elsőbbséget élvezett az aritmetikával szemben, abban az értelemben, hogy a legtöbb aritmetikai fogalmat geometriaira vezettek vissza. Kialakult a matematikai tétel fogalma, mely egyfajta általánosságot kifejező matematikai kijelentés, szemben a tapasztalattal és az esetleges megállapításokkal. Amikor valaminek a létezését kívánták megmutatni, akkor azt főként elemi geometriai úton tették, mely eljárást szerkesztésnek, konstrukciónak neveztek. A szerkesztéshez csak körzőt és vonalzót használtak. A tételek igazságának felismerési módja – a „belátás” és „megmutatás” – ábrák segítségével átélhető vizuális élmény, amely még nem a levezetés, de már az általánosság fennállásának gondolati úton történő igazolása volt. A geometriában ez ábrákkal, a számtanban kavicsokkal történt.
Thalész bizonyítási módszere a „kongruenciabizonyítás” volt, melynek alapelve az egybevágóság, illetve az átdarabolhatóság. Ezek lényegében véges, konstruktív (a gyakorlatban végrehajtható) bizonyítási eljárások. Síkgeometriai bizonyításait akár papírlappal, ollóval, az alakzatok kivágásával és egymásra helyezésével is elvégezhetnénk.
Az első időszak Pithagorasz iskolájának megjelenésével zárult le, és kezdetét vette az aritmetika korszaka. A püthagoreusok világképük alapjául a számokat választották. A világegyetem harmóniáját a számok tökéletességével kapcsolták össze. Aritmetikai szemléletre épülő matematikaképük akkor került válságba, amikor bebizonyosodott, hogy a négyzet átlójának és oldalának aránya nem fejezhető ki két egész szám hányadosaként, azaz nem aritmetikai fogalom. A megoldást az aritmetika újbóli geometrizálása jelentette, mely a knidoszi Eudoxosz megalkotta arányelméleten alapult.
A deduktív matematika hajnala (Kr.e. VI–IV. sz.)
Az éleai filozófia, Parmenidész és az éleai Zénón hatására megjelent az igény a deduktív bizonyításra. Filozófiai okokból az indirekt bizonyítást tekintették az igazság egyedüli kifejezési módjának. A legkorábbi deduktív értekezés Eukleidész Elemeinek a párosról és páratlanról írt részének keletkezése, melyet feltehetően még a pithagoreusok alkottak. Az absztrakt bizonyítás módszerének hatékony alkalmazása vezetett el ahhoz a felismeréshez, hogy a négyzetgyök kettő nem racionális szám (inkommenzurábilis arány). A számfogalom biztos alapra helyezése végett ebben az időben keletkezett Eudoxosz arányelmélete, mely később történeti alapját képezte Dedekind, a valós számok halmazelméleti definíciójára vonatkozó kutatásainak. A deduktív matematika és a logika kezdetei tehát összekapcsolódnak a görög matematika újbóli geometrizálódásával.
Platón ideatana adott először magyarázatot a matematikafilozófia egyik legfontosabb kérdésére, mégpedig hogy miből ered a matematikai tételek nagyfokú objetkivitása. Platón szerint „árnyékvilágban” élünk, tárgyaink, fogalmaink nem valóságosak. A valóságos létezők az ideák világában keresendők. Amikor geometriai alakzatokról fogalmazunk meg tételeket, akkor valójában felfedezzük az ideális világ, ideális alakzatainak tulajdonságait. A matematikai fogalmak ideáinak létezéséből következik, hogy minden ember ugyanazokat a matematikai kijelentéseket tekintheti csak igaznak. Platón ezzel a gondolattal megalapozta azt a filozófiai álláspontot, melyet a 21. században a jelentés referenciális elméletének, vagy metafizikai realizmusnak nevezünk. Ennek matematikai válfaja a matematikai realizmus, melyre gyakran hivatkoznak úgy, mint platonizmus, ami rendkívül erős elmélet, habár kritikusainak ellenérvei sem gyengébbek.
Eukleidész és kora (Kr.e. IV. sz.)
A matematikai tudást rendszerezett formában tankönyvekbe foglalták, melyek címe Elemek (ti. a geometria és az aritmetika tudományának elemei) volt. Az egyetlen fennmaradt ilyen összefoglaló mű Eukleidész Elemek c. könyve (feltehetőleg azért, mert ez volt a legjobb, így ez volt a legnagyobb példányszámú). A deduktív tárgyalásmód hármas talapzaton nyugvott: definíciók, posztulátumok és axiómák. Az axiómák olyan állítások, melyeket a korban evidensnek tartottak, a posztulátumok ezzel szemben egyesek által vitatott, de Eukleidész által „megkövetelt” kiinduló állítások voltak. Eukleidész idejére a konstruktív módszer (ábrák és szerkesztés) egyensúlyba került az indirekt bizonyítással (redukció ad abszurdum – visszavezetés a lehetetlenre). Például mind a Thalész-tételt, mind a Pithagorasz-tételt átdarabolással (vagy átdarabolásra visszavezethető módon) igazolták, mely bizonyításban nagy szerepet kapott az ábra. Megfordításukat viszont indirekt látták be, amely a logika nem csekély ismeretéről árulkodik. Erre a korszakra vezethető vissza a klasszikus logika azon álláspontja, mely szerint valamely matematikai objektum létét úgy is lehet igazolni, hogy mutatunk rá példát, de úgy is, hogy nem létezésének feltételezéséből ellentmondsára jutunk. Ekkor foglalja össze Arisztotelész az Organonban a klasszikus logika alapelveit, és mutat rá annak korlátaira.
Késői görög matematika (Kr.e IV. sz. – Kr.u. IV. sz.)
Arkhimédész fizikai szemlélettel állt hozzá a tételek felismeréséhez. Ezzel ő volt a heurisztikus módszer (és Pólya György heurisztikájának) előfutára, a felfedezés és intuíció fontosságát hangsúlyozta. Olyan intuitív és újszerű gondolatokkal közelített a geometriához, ami nem cáfolt rá feltaláló mivoltára. A szakaszokban emelőket, a háromszögek középpontjában súlypontot látott. A görbevonalú síkidomok területét annak végtelen sok végtelenül keskeny sávra bontásával számította ki. Ugyanezt a pergai Apollóniosz végtelen közelítő mértani összeggel határozta meg.
Papposz matematikatörténeti művet írt. Összefoglalta a matematika módszertanát, amelyben lényeges szerepet szánt a heurisztikának. Megfogalmazta a párhuzamossági axióma (Eukleidész V. posztulátumának) egy átfogalmazását. Célja – mint sok elődjének – az volt, hogy az ötödiket megpróbálja levezetni az első négy posztulátumból. Ezenkívül Papposz rámutatott arra, hogy a matematikai tételeknek mindig meg kell vizsgálni a megfordításukat. Akkor jutunk ugyanis előbbre a tétel megértésében, ha megismerjük egyrészt minden lényeges következményét, másrészt mindent amiből következik. A leghasznosabb a tétel megértésében viszont az, ha minél több ekvivalens megfogalmazására bukkanunk. Ezzel Papposz a matematikai kijelentések jelentésének egyfajta – nem feltétlenül platonista (mai elnevezéssel verifikacionista) – meghatározását adta.
Az újkor matematikafilozófusai (XVI–XVIII. sz.)
Galilei az eukleidészihez hasonló módon rendezte deduktív rendszerbe a kinematikáról írt művét. Felfedezte a végtelennel kapcsolatos, már Zénónnál is megjelenő paradoxont, ami szerint „a rész egyenlő az egésszel”. Ez a felismerés a XIX. században Cantornál jött elő újra, mint a végtelenség definíciója. Galilei úgy tartotta, hogy a matematika a természet nyelve.
Descartes megírta Értekezések a módszerről című könyvét, amelyben megfogalmazta a tudományos kutatás máig érvényes kritikus alapállását. Eszerint:
1. Semmit ne fogadjunk el igaznak, míg annak igaz, vagy evidens voltáról meg nem győződünk. Ne tegyünk elhamarkodott tudományos kijelentéseket.
2. A kutatás tárgyát annyi gondolati egységre osszuk, ahányra csak lehet, az alapos és kimerítő tárgyalás érdekében.
3. Az érvelésnek rendszerezettnek kell lennie. Az felépítésnek az egyszerűbb fogalmaktól az összetettebbekig kell haladnia.
4. Mindenütt teljes felsorolásra, általános kijelentések megfogalmazására törekedjünk.
Descartes mindazonáltal már a Módszerről geometriai részében sem vitte végig következetesen gondolatmenetét. Tárgyalásmódja nem volt deduktív, megállapításai nem levezetéssel, hanem esszészerű formában keletkeztek, diszkussziói, felsorolásai nem voltak teljesek. Ez azonban nem azt jelenti, hogy ne gondolta volna komolyan a kutatás módszerét, és az ne lenne ma is érvényes. Itt inkább az a furcsa kettősség mutatkozik meg, ami szinte mind a mai napig él a matematikában. Lakatos Imre rámutatott, hogy a tételek és bizonyítások evolúciószerűen fejlődnek a matematikus elméjében és a matematikatörténetben. A deduktív bizonyítás csak ennek végállapotát tükrözi és az érvényességet, igaz voltát biztosítja, de semmit nem mond a matematikai fogalmak értelméről, jelentéséről és fejlődéséről.
Spinoza volt az első, aki szétválasztotta a matematika filozófiáját a teológiától. A pithagoreus és platóni hagyomány a matematikát az isteni rend kifejeződéseként tekintette, mely szerint az isteni törvények következménye a matematikában található rend és objektivitás. Descartes és Leibniz megfordította a gondolatmenetet. Szerintük a matematika és a logika kétségbevonhatatlan tényei igazolni tudják Isten létét. Spinoza rámutatott arra, hogy a matematika objektivitása és kristálytisztasága nincs kapcsolatban a teológiai kérdésekkel. A tudománynak a teológiai és tekintélyektől független módon kell hogy kutassa a természeti törvényeket.
Leibniz megpróbálta az arisztotelészi logikát formulákban kifejezni. Megalkotta a calculi universalist, illetve a lingua universalist, az „egyetemes nyelvet”, ami a tudományok általános leírására lett volna hivatott.
Kant a matematikát az a priori / a posteriori és analitikus/szintetikus dimenziókban helyezte el. Szerinte a matematika állításai szintetikus és a priori állítások. Szintetikusak, amennyiben igazságuk nem evidens, a bennük előforduló fogalmak immanens tulajdonsága, hanem belátásuk gondolati műveleteket (deduktív út) igényel; a prioriak, amennyiben nem a tapasztalat alapozza meg igazságukat, hanem a belső intuíció.
Modern matematikafilozófia a XIX. században
A matematika módszertana a XIX. század elején gyökeresen megváltozott. Újrafogalmazódtak a bizonyítással szemben támasztott követelmények, és a középkori felfogáshoz képest az axióma fogalma is lényeges jelentésváltozáson ment keresztül. Mindezek hatására kialakult a modern logika és a modern matematikafilozófia.
„A szigorúság forradalma”
XIX. század közepén (az 1850-es, 60-as évekre) – főleg Cauchy és Weierstrass munkásságának köszönhetően – kialakult a bizonyítások olyan szigorú elemzésének módja, mint amelyet ma is tapasztalunk, ha kinyitunk egy felsőbb szintű matematikáról szóló könyvet. A bizonyításelemzés szigorúbbá válásának szükségszerű velejárója a rejtett előfeltevések kimutatása és a matematikai fogalmak definícióinak pontosítása volt. Lényegében ennek, a matematikára azóta is jellemző pontosságnak a megjelenését nevezzük (Lakatos Imre kifejezését használva) a szigorúság forradalmának. Néhány pontban áttekintjük, hogy miért vált szükségessé ez.
Ellenpéldák az analízisben
A XVII. században létrejött differenciál- és integrálszámítás (közös nevén analízis, régebben „infinitezimálszámítás”) rendkívül hatékony módszernek mutatkozott a fizikában. Az égi mechanika XVIII. századi diadalában az analízis is osztozott. Segítségével percre pontosan előre lehetett jelezni a bolygók, holdak és üstökösök mozgását.
Az analízis a matematika komoly alapágává vált. Éppen ezért volt meglepő, mikor később sorra felbukkantak olyan ellenpéldák, amik az analízis általános tételeinek érvényességét látszottak szűkíteni. (Ilyen volt például Abelnek (1826) a folytonos függvények konvergens sorozatáról szóló tételhez gyártott ellenpéldája.) Sokan – a legnevesebb matematikusok, az analízis „nagy öregjei” közül is – úgy gondolták, hogy ezek hajuknál előrángatott dolgok, puszta agyszülemények, amik a matematika valóságára nincsenek hatással. Természetesen ezen a ponton a tudományos diskurzus megszűnne, de voltak, akik komolyan vették a cáfolatokat, és megpróbáltak a bizonyítások mélyére tekinteni, hogy felleljék a hibákat vagy pontatlanságokat. Végül ez utóbbi (a tudományosabb) vélemény hívei győzedelmeskedtek.
Megjegyzés: Nem kell azt gondolnunk, hogy az analízis tételeit ugyanazok a matematikusok, akik a számelméletben nagy pontossággal tevékenykedtek, elhanyagolták. A pontatlanság oka nem a kor matematikusaiban keresendő. Az aritmetika sokkal biztosabb fogalmi háttérre épült, mint a végtelen kicsiny és végtelen nagy számok intuitív fogalmát használó analízis. A természetes számok kavicsmodellje sokkal ellenőrizhetőbb kép, mint a végtelen kicsiny mennyiségek intuitív képe. Mindazonáltal tény, hogy az intuitív gondolkodás sikere az analízisben megrészegíthette a kutatókat. Ahogy D'Alembert mondta: „Előre a felfedezés útján! Az igazolást majd az utókor elvégzi.” Az ilyen úttörők meglepetésére, az utókor több esetben nem az igazolást, hanem a cáfolást végezte el – ha nem is az eredmények helytelenségét, de az érvelések támadhatóságát leleplezve.
Bizonytalanságok a geometriában
Kiderült, hogy az ellenpéldák felbukkanása nem korlátozódik az analízisre. Az Euler-féle poliédertételre is találtak cáfoló szituációt. Galois (1829) nemszerkeszthetőségi tételei rámutattak arra, hogy az irracionális számok elméletének megalapozása sem geometriailag, sem aritmetikailag nincs jól kivitelezve. Ha ugyanis nem szerkeszthető meg minden irracionális szám hosszúságú szakasz az egyenesen, akkor mik az irracionális számok?
A „paralellák problémájának” megoldása is váratott magára, mely a párhuzamossági axiómának a többi eukleidészi axiómából történő levezetését tűzte ki célul. Korszakalkotó meglátása a kérdésben Bolyai Jánosnak (1832) támadt. Akár ellentmondásra vezet a párhuzamossági axióma tagadása, akár nem, a geometria számára biztos alap a párhuzamossági axiómát mellőző, maradék axiómarendszer (feltéve, hogy az euklideszi geometria ellentmondásmentes, bár ezt a korban a szemléletből adódóan evidenciának tartották). A „biztonságos” maradék axiómarendszerben felépített geometriát nevezte Bolyai abszolút geometriának. Felvetődik azonban a kérdés: léteznek-e egyáltalán ilyen nemeuklideszi geometriák?
A matematika megalapozásának paradigmája
Miután a bizonyításelemzés módszerét sikerült megszigorítani, és az analízis alapfogalmait is visszavezették az aritmetikára (ezt nevezzük az analízis aritmetizálásának), megfogalmazódott az az igény, hogy a teljes matematikát biztos alapokra kell helyezni. Ezt az álláspontot nevezik a matematika megalapozási paradigmájának. Hatására létrejöttek a matematikában később matematika alapjai (metamatematika) néven összefoglalt tudományterületek. Feladata olyan egységes elmélet keresése lett, melynek keretein belül az egész matematika ellentmondásmentesen elhelyezhető. Természetesen a matematika alapjainak kutatása nem mentes a világnézeti (metafizikai, pragmatikai, stb.) vonatkozásoktól, nézetektől. Ezért vitatható, hogy – legalábbis célkitűzéseit tekintve – teljesen matematikai természetű résztudománynak mondható-e. Mindazonáltal kétségtelen, hogy az ezen a területen dolgozó matematikusok tevékenységük során komoly eredményeket értek el. Elsőként Dedekindnek a valós számokkal kapcsolatos vizsgálatai voltak nagy jelentősségűek. Visszanyúlt Eukleidész arányelméletéhez, s az irracionális számok elméletét viszavezette az aritmetikára (1872, 1888).
Cantor megalkotta a halmazelméletet (1874), mely kiváló segédeszköznek bizonyult a végtelen halmazok, így a számok, a sík és a tér vizsgálatához. Cantor halmazelmélete – a később naiv halmazelméletnek nevezett elmélet – jó eséllyel pályázhatott a megalapozási paradigma hívei által áhított „szuperelmélet” helyére.
Megjegyzés: A megalapozási paradigma – melyet gyakran a kissé pejoratív csengésű fundacionalizmus (sőt: „fundamentalizmus”) elnevezéssel illetnek támadói –, sem napjainkban nem osztatlanul elfogadott elv, sem a XIX. században nem volt az. Az antifundamentalisták például bizonyos metamatematikai tételekre hivatkozva lehetetlennek tartják, hogy a matematika egyetlen elméleten belül elhelyezhető legyen. Azonban tény, hogy a megalapozási elv régebben a matematikafilozófia fősodorbeli áramlatát jelentette, és ma is ez az elv húzódik meg a legtöbb matematikafilozófiai vizsgálódás hátterében.
Frege logicista programja
Cantor naiv halmazelmélete lényegében tisztán logikai fogalmakra épül (mint például a predikátum és igazságtartománya). Ha tehát Cantor halmazelméletének eszközeivel sikerül a matematikát leírni, akkor kijelenthetjük, hogy a matematika a logika része. Természetesen, amennyiben a logika szabályain kívül további előfeltevéseket kell tennünk, ahogyan ezt tesszük is az euklideszi geometria axiómáiban, akkor máris nem állíthatjuk, hogy a kérdéses elmélet tiszán logikai. Gottlob Frege volt az, aki megmutatta, hogy ha a geometriát nem is, de az aritmetikát ki lehet fejezni – a naiv halmazelmélet segítségével – tisztán logikai terminusokban, mindenféle matematikai természetű axióma feltételezése nélkül. Az olyan kezdeményezéseket, melyek a matematikát a logikára kívánják visszavezetni, logicista álláspontoknak nevezzük.
Az aritmetika logikai megalapozása
Frege álláspontját és kivitelezésének módját Az aritmetika alapjai című könyvében fejti ki. Alapgondolata a természetes számok definíciójára a mai átírásban a következő volt. A nullát úgy definiálta, mint az összes olyan halmaz halmaza, melynek nincs eleme. Természetesen van ilyen halmaz, mert például az {x|„x nem egyenlő x-szel”} halmaz üres (a jelölések értelmét lásd a naiv halmazelmélet szócikknél). Az 1-et úgy definiálta, mint az összes olyan halmaz halmaza, mely azonos számosságú egy egyelemű halmazzal. Egyelemű halmaz szintén létezik, mert mondjuk az {x|x=0} halmaz egyelemű. Hasonlóképpen definiálta az összes természetes számot egy induktív definíció segítségével. Frege volt az első, aki a természetes számokat halmazelméleti fogalmak segítségével definiálta.
A formalista ideológia elterjedése
Ha meg tudnánk kérdezni arról Fregét, hogy munkásságában mit ítél a legjelentősebb alkotásnak, akkor bizonyára az aritmetika logikai megalapozása lenne a válasz (ez a kérdés persze több szempontból is rossz). Az utókor mégis Frege logikában elért eredményeit méltányolja leginkább. Frege korszakalkotó módon megalkotta a formális logikát. Célja, hogy a rejtett lemmákat, ki nem mondott előfeltevéseket úgy mutassa ki, hogy a bizonyítást elemi következtetési lépések formális láncolataként írja le. Eközben csak olyan kifejezéseket szerepeltet, melyeket addig már definiált. Vegyük észre, hogy ez a program Descartes módszerének a végső határig feszített kivitelezése. Egy elméletet szavakra, mondatokra bont le és az elmélet értelmét és a mondatok igazságát ez alapján próbálja feltárni. Nem véletlen, hogy Fregét tartják az modern analitikus nyelvfilozófia megteremtőjének. Amennyiben sikerül a bizonyításokat ezen a formális matematikai nyelven leírni, akkor elérjük a teljes bizonyosságot, abban az értelemben, hogy a formalizáció során semmilyen megalapozatlan állítás felhasználására nem lesz módunk.
A matematika és a logika egyes részterületeinek formalizálására már korábban is tettek erőfeszítéseket. Leibniz az általa calculi universalisnak nevezett formális nyelvében megkísérelte formalizálni az arisztotelészi logikát (1714). George Boole formalizálta a kijelentéskalkulust, és adott hozzá egy algebrai, egy logikai, egy valószínűségelméleti és (tanítványa, Venn jóvoltából) egy geometriai interpretációt (1854). Úgy gondolta, hogy ezzel megteremtette a matematika egységes leírását. Később Peano formalizálta az aritmetikát (1896). Munkája sokkal ismertebb volt, mint Fregéé, így Peano jelölésrendszere terjedt el. Mindazonáltal Frege rendszere sokkal általánosabb érvényű volt, filozófiai és logikai kidolgozottságát tekintve pedig messze Peano elmélete előtt járt. Frege műveire csak később, Russell hívta fel a figyelmet.
Peano, Frege és Russell hatására a megalapozási paradigma kibővült a formalista szemlélettel. A „szigorúság forradalma” által a bizonyításelemzésre rótt teher súlyát némiképp könnyítette, hogy az elfogadható érveléseket a formális logika összegyűjtötte. A bizonyítások formalizálásával azok helyességét elvileg „teljes bizonyossággal” megállapíthatjuk. Ezért a megalapozást megvalósító elmélet keresése valójában egy formális nyelvi megalapozó elmélet keresésévé alakult árt.
A megalapozási elv első válsága
A naiv halmazelmélet ellentmondásai gyorsan napvilágot láttak. Először Cantor szembesült ellentmondással (Cantor-antinómia), de ezt csak később, a Burali-Forti-antinómia napvilágra kerülése (1897) után publikálta. A Russell-antinómiát először Frege Az aritmetika alapjai II. című műve utószavából ismerhette meg a nagyközönség (1902). A matematikatörténet nevezetes pillanata volt, amikor Frege érzéseit a következő latin mondást idézve fejezte ki:
- „ Solatium miseris, socius habuisse malorum.”
- [A szerencsétlen vigasza, ha társai vannak a bajban.]
A paradoxonok ugyanis Cantor, Dedekind és Russell eredményeire is negatív kihatással voltak. A megalapozási elv híveinek feladatává ezek után a paradoxonok kiigazítása vált.
Matematikafilozófia a XX. század első felében
A naiv halmazelmélet antinómiáinak feloldására számos elmélet készült, ezek közül három különösen fontos, mert irányadónak számít három markánsan különböző matematikafilozófiai áramlat számára.
Russell logicista programja
Russell azon kívül, hogy mentesíteni akarta Cantor elméletét az ellentmondásoktól, célul tűzte ki, hogy megmenti Frege logicista programját. Formális logikai elmélete, a típuselmélet és az elágaztatott típuselmélet számos addig fellépő logikai paradoxont kiküszöböl (így például a Russell-paradoxont és a definiálhatóság Grelling-Nelson-paradoxonát). Célja azonban ennél sokkal több volt. A Whiteheaddel közösen megírt Principa Mathematica című könyvében részletesen kifejti, hogy miként lehet a típuselméletben rekonstruálni a matematika alapjait, ezzel visszavezetve a matematikát a logikára. Meg kell azonban állapítani, hogy kísérlete koránt sem tekinthető sikeresnek. Ahhoz, hogy akár csak a természetes számokat definiálni tudja a típuselméletben, fel kellett tennie az úgy nevezett végtelenségi axiómát. Ezzel viszont pont egy olyan nemlogikai előfeltevést épített be rendszerébe, mely kétségessé teszi azt az kijelentést, hogy a matematikát tisztán a logika következményeként tekinthetjük.
A típuselmélet ugyan alkalmazásra talált a formális logikában, de mint a matematika alapjainak formális nyelvi megalapozása nem járt sikerrel. A matematikusok túl nehézkesnek találták a típusok rendszerét. Russell azonban sokkal nagyobb befolyásra tett szert a matematika filozófiájában. Nem kevéssé személyes tekintélyének köszönhetően szinte máig uralkodó az angolszász nyelvterületeken az a felfogás, miszerint a matematikafilozófia russelli tárgyalása az analitikus filozófia mintapéldája. A filozófia nem lehet más, mint a tudományok filozófiáinak összessége, a tudományfilozófiákat pedig az analitikus filozófia eszközeivel, a logikára alapozott nyelvfilozófia eszközeivel kell művelni. Ennek a legkönnyebben kivitelezhető esete a matematika filozófiája, hiszen a matematikában nyilvánul meg legtisztábban a helyes következtetés. Az analitikus filozófia központi problémája a nyelvi elemek jelentésének feltárása. A logikára és a logikára visszavezetett, általa tiszta matematikának nevezett formális matematikára vonatkozóan a jelentés elmélete azonban elég kilátástalan képet fest. Russell szerint:
- „A tiszta matematikában sem azt nem tudjuk, hogy miről beszélünk, sem azt, hogy igazat mondunk-e vagy sem.”
Ugyanis a formuláknak önmagukban semmi kapcsolatuk a valósággal, a matematikában az axiómákat pedig önkényesen választjuk. Bár logicista programja nem tartható, mindamellett az analitikus filozófia alkalmazásával Russell a formalista-konvencionalista irányzat megteremtőjévé vált.
Hilbert finitizmusa
A halmazelmélet Zermelo–Fraenkel-axiómarenszerének sikeres bevezetése után nyilvánvalóvá vált, hogy jól működő módszer a matematikában a részterületek formális-axiomatikus elméletekké alakítása, azaz a formalizáció. Az axiómarendszerek „jóságának” kritériuma az, hogy ellentmondásmentesek és negációteljesek legyenek. Circulus vitiosushoz vezethet azonban belátni a halmazelmélet ellentmondásmentességét, ha halmazelméleti eszközökkel tesszük azt. Hilbert szerint olyan bizonyításokat kell használni, melyben a megengedett eszközök már biztos szemléleti alapon nyugszanak és nem feltételezik a végtelen számosságok végtelen hierarchiáját, melyeknek létét a korban sokan kritizálták. Hilbert a matematikai bizonyosság legelemibb, legkétségbevonhatatlanabb szintjeként a finit aritmetikát nevezte meg. A finit aritmetika olyan számelmélet, melyben számok semmilyen végtelen halmazára, mint totális egészre nem hivatkozunk. Ez lenne a biztos alap a matematika megalapozásához, illetve a ellentmondásmentességi bizonyítások elvégzéséhez. Kétséges volt azonban magának a Peano-aritmetikának is az ellentmondásmentessége. Több más jellegű problémával együtt ezen elmélet ellentmondásmentességi bizonyítását is feladatként fogalmazta meg a matematikustársadalom számára, az úgy nevezett Hilbert-program keretein belül.[5]
Ahogy Russell analitikus filozófiát csinált a matematikafilozófiából, úgy Hilbert, a matematikus, matematikai princípiává kívánta tenni. Szerinte a matematika filozófiája a matematika formális rendszereinek matematikája, az általa metamatematika névvel illetett terület. Feladata az ellentmondásmentességi, a nemteljességi és a függetlenségi vizsgálatok elvégzése. Ugyanúgy, ahogy Russell típuselméletét sikerrel alkalmazta a formális logika, a metametematika tételei a matematikai logikának váltak komoly eredményeivé. Hilbert formalizmusa azonban kölönbözik Russell formalista-logicista irányvonalától. A matematika jelentését ugyanis Hilbert a finit matematikából kívánta származtatni, így egyáltalán nem gondolta jelentés nélkülinek. Finitista ideológiája azonban nem vált uralkodóvá, és formalista hozzáállását is sokan eredménytelennek itélik.
Intuicionizmus, konstruktivizmus
Brouwer holland matematikus és filozófus elvetette a matematikafilozófia analitikus filozófiai szemléletét, és tagadta a formális nyelvi vizsgálatok matematikán belüli elsődlegességét. Szerinte a bizonyosság a „matematikai intuícióból” származik, melynek legalapvetőbb momentuma a természetes számok rákövetkezés útján történő keletkezése.
- „Az intuicionista matematika lényegében nyelv nélküli tevékenység, melynek eredete az idő elmozdulásának érzékelése, ti. annak, hogy egy életmozzanat két különböző dologra esik szét, melyek közül az egyik utat enged a másiknak, de megmarad az emlékezetben. Az így megőrzött kettősség a matematika alapintuiciója.” Brouwer
A természetes számok ezáltal egyfajta szüntelen keletkezés állapotában vannak, kizárva az intuicionista számára a totális (vagy aktuális) végtelen önállóan létezőként való elfogadását. Minden matematikai objektumot a természetes számokra kell visszavezetni, mégpedig úgy, hogy az illető objektumhoz véges sok lépésben eljuthassunk (konstrukciók). Az intuicionizmus nem fogadja el az indirekt egzisztenciabizonyításokat – vagyis az olyan bizonyításokat, melyek egy dolog létét azzal igazolják, hogy belátják: nemléte ellentmondásra vezet. Ekkor ugyanis nincs feltétlenül meg a közvetlen kapcsolat a természetes számokkal. Ebből viszont az is következik, hogy nem teljesülhet a kizárt harmadik elve.
Időrendileg az intuicionizmus eszméje a hilberti finitizmus előtt született meg. Hermann Weyl, Hilbert tanítványa kacérkodott az intuicionista gondolat elfogadásával, ennek eredményeképpen jutott Hilbert arra az elhatározásra, hogy szükséges magának is kialakítania egy filozófiailag elfogadható, de a matematikai gyakorlathoz is jól illeszkedő matematikafilozófiát.
A megalapozáselv második válsága
Miközben dúlt a szellemi harc az axiómarendszereket relativizáló hilberti és russelli formalizmus, illetve az emberi tényezőt is előtérbe hozó intuicionizmus között, aközben megszületett a modern matematikafilozófia egyik legnagyobb eredménye, Gödel első és második nemteljességi tétele (1931). Gödel tételei csapást mértek – bár nem egyértelmű, hogy mekkorát – mindenféle megalapozási elvre.
Az első tétel következményei
Gödel első nemteljességi tétele azt mondja ki, hogy:
- Minden ellentmondásmentes, a természetes számok elméletét tartalmazó, formális-axiomatikus elméletben megfogalmazható olyan mondat, mely se nem bizonyítható, se nem cáfolható.
Hilbert az aritmetika ellentmondásmentességének bizonyítását a matematikustársadalom számára feladatul tűzte ki. Hasonlóképpen elvárásai közé tartozott, hogy az aritmetikában minden állítás igazságát el tudjuk dönteni levezetéssel. Ezek az igények tehát azt jelentik, hogy:
1. szükséges bebizonyítani, hogy hamis állítást nem vezethetünk le az aritmetika axiómarendszeréből (ellentmondásmentesség)
2. legyen olyan axiómarendszere az aritmetikának, melynek nyelvén minden megfogalmazott kijelentés vagy igazolható vagy cáfolható (negációteljesség).
Gödel tétele szerint ez egyszerre nem teljesülhet, mert az aritmetika vagy ellentmondásmentes, vagy negációteljes. Sőt, minden nemtriviális axiomatikus elmélet esetén fennáll a bizonyosságnak eme hiánya. Durván fogalmazva: feltéve, hogy egy matematikai elmélet ellentmondásmentes, mindig megfogalmazható lesz benne olyan eldöntendő kérdés, melyre nem létezik válasz. Amennyiben a tételnek ezt az interpretálását elfogadjuk, az a matematika egy elég zavarbaejtő jellegére mutat rá.
A második tétel következményei
Gödel második nemteljességi tétele azt mondja ki, hogy:
- Ellentmondásmentes, a természetes számok elméletét tartalmazó, formális-axiomatikus elméletben az „ez az elmélet ellentmondásmentes” mondatnak megfelelő formális kijelentés nem bizonyítható.
A második tétel megítélésében centrális kérdés, hogy az „ez az elmélet ellentmondásmentes” aritmetikai kijelentésnek milyen jelentést tulajdonítunk. A következő – nem nyilvánvaló – értelmezés azonban sokkal súlyosabb következményekkel jár, mint az első tétel esetén.
- T ellentmondásmentességét nem lehet egy T-vel azonos, vagy gyengébb formális elméletben igazolni.
Tegyük fel, hogy a T formális-axiomatikus elmélet ellentmondásmentességét szándékozunk bizonyítani. Ezt a bizonyítást a T tárgyelmélet egy szintén formális-axiomatikus 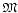 metaelméletében tesszük meg, például olymódon, hogy belátjuk egy konkrét S tárgynyelvi mondatra hogy ez nem bizonyítható T-ben (ez ugyanis elegendő T ellentmondásmentességéhez). Ha metaelméletében tesszük meg, például olymódon, hogy belátjuk egy konkrét S tárgynyelvi mondatra hogy ez nem bizonyítható T-ben (ez ugyanis elegendő T ellentmondásmentességéhez). Ha 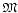 nem erősebb mint T, akkor nem erősebb mint T, akkor 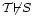 megfogalmazható T-ben és kapjuk a megfogalmazható T-ben és kapjuk a  formulát. Ha ebből következik formulát. Ha ebből következik 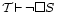 , akkor rögtön ellentmondásra jutunk, hiszen Gödel második nemteljességi tétele szerint ekkor (lévén T ellentmondásmentes) , akkor rögtön ellentmondásra jutunk, hiszen Gödel második nemteljességi tétele szerint ekkor (lévén T ellentmondásmentes) 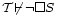 . .
Az aritmetikát minden megalapozási célra szánt matematikai elméletnek tartalmaznia kell, így ellentmondásmentességének bizonyítását eszerint nem lehet semmilyen azonos erősségű metaelmélet alapján bebizonyítani. Speciálisan: az aritmetika ellentmondásmentességét nem lehet aritmetikai eszközökkel bizonyítani – ahogy azt Hilbert szándékozott volna. (Megjegyezzük, hogy az aritmetika ellentmondásmentességére transzfinit bizonyítást azonban már talált Gerhard Gentzen 1936-ban.)
Ez a negatív eredmény sokkolta az addig a matematika megalapozásáról élénk diskurzust folytató matematikafilozófiával is foglalkozó matematikusokat. Jól illusztrálja a 20-as, 30-as évek hangulatát Neumann János, aki könyvében, miután hosszasan leírja a történteket, így összegez:
- „Azért meséltem el ennek a vitának a történetét ilyen részletesen, mert úgy hiszem, ennél jobban nem is lehetne óvatosságra inteni az embereket, nehogy túlságosan készpénznek vegyék a matematika rendíthetetlen szigorát. Mindez a mi korunkban történt, és magamról tudom, hogy ebben a korszakban az abszolút matematikai igazságról vallott saját nézeteim is milyen szégyenletes sebességgel változtak, volt, hogy egymás után háromszor is!”
- A mai matematikafilozófia áramlatairól lásd: matematikafilozófia.
Matematikafilozófia
A matematikafilozófia a filozófia, ezen belül a tudományfilozófia azon ága, mely a matematikával foglalkozik (szemben a tudománnyal mint olyannal általában foglalkozó tudományfilozófiával, melynek nem tárgya külön a matematika természete, és ami nem jelenti külön egy-egy tudományág vizsgálatát, a matematikafilozófia az ún. genitivus-filozófiák közé tartozik, és a matematika filozófiai vonatkozásaival foglalkozik. Lényegében ugyanolyan résztudományokra bontható, mint maga a tudományfilozófia, kiegészítve egy-egy speciális területtel.
A matematikafilozófia főbb területei
- Metafizikai természetű kérdések
- Mik a számok? Mi a pont, az egyenes, a sík? Mi a halmaz? Mi a jelentése a matematikai tételeknek, fogalmaknak?
- Mindig is léteztek matematikai természetű objektumok (azaz felfedezhetők), vagy fel kell őket találni? Biztosan létezik egy matematikai objektum, amit meg tudunk nevezni, vagy meg is kell azt alkotnunk (konstruálnunk)? Létezik-e végtelen?
- Episztemológiai problémák
- Mi a matematikai igazságok felismerésének módja? Milyen módon juthatunk el az igazsághoz? Dedukcióval vagy heurisztikus módon jutunk-e el a tételekhez? Eljuthatunk-e a teljes igazsághoz? Vannak-e korlátai az emberi elmének?
- A tudománymetodológia kérdései
- Mik a matematikai érvelések elfogadott formái? Hogyan szervezzük rendszerbe a matematika tudományát? Mi a matematika tudománya? Mitől működik a matematika (azaz miért alkalmazható olyan jól a fizikában és a műszaki tudományokban)?
- Metamatematika - A matematika megalapozásának problémái
- Mire épül a matematika? A logikára? Ha az nem elég, akkor milyen elmélettel kell kiegészítenünk a logikát, hogy minden matematikai területet elérhessünk egy egységes elmélet keretei között?
- Ha a matematika területei formális, axiomatikus, deduktív rendszerek, akkor bebizonyítható-e az ellentmondásmentességük? Meddig terjed a kifejezőképességük? Miért pont azok az axiómák, amik? Adekvát módon írják-e le a formális rendszerek az elméletek szándékolt jelentését?
Matematikafilozófia a Gödel tételek után
A modern matematikafilozófia egyik legnagyobb eredménye Gödel első és második nemteljességi tétele (1931). Gödel tételei csapást mértek - bár nem egyértelmű, hogy mekkorát - mindenféle megalapozási elvre.
Az első tétel következményei
Gödel első nemteljeségi tétele azt mondja ki, hogy:
- Minden ellentmondásmentes, a természetes számok elméletét tartalmazó, formális-axiomatikus elméletben megfogalmazható olyan mondat, mely se nem bizonyítható, se nem cáfolható.
Hilbert az aritmetika ellentmondásmentességének bizonyítását feladatul tűzte ki a matematikustársadalom számára. Hasonlóképpen elvárásai közé tartozott, hogy az aritmetikában minden állítás igazságát el tudjuk dönteni levezetéssel. Az tétel szerint ez egyszerre nem teljesülhet. Sőt, minden nemtriviális axiomatikus elmélet esetén fennáll a bizonyosságnak eme hiánya. Durván fogalmazva: feltéve, hogy egy matematikai elmélet ellentmondásmentes, mindig megfogalmazható lesz benne olyan kérdés, melyre nem létezik válasz. Amennyiben a tételnek ezt az interpretálását elfogadjuk, az a matematika egy elég zavarbaejtő jellegére mutat rá.
A második tétel következményei
Gödel második nemteljeségi tétele azt mondja ki, hogy:
- Ellentmondásmentes, a természetes számok elméletét tartalmazó, formális-axiomatikus elméletben az 'ez az elmélet ellentmondásmentes' mondatnak megfelelő formális kijelentés nem bizonyítható.
A második tétel sokkal súlyosabb következményekkel jár. Tegyük fel, hogy a T formális-axiomatikus elmélet ellentmondásmenteségét szándékozunk bizonyítani. Ezt a bizonyítást a szintén formális-axiomatikus T ' (meta)elméletben tesszük meg. Legyen ennek a Cons(T): 'T ellentmondásmentes' mondat bizonyításának formalizált változata a T ' -beli p lépéssorozat. Ha a p bizonyítás elvégzéséhez szükséges elméleti háttér azonos erősségű a T elmélettel, azaz p lefordítható T nyelvére, akkor T-ben megfogalmazható és bizonyítható lesz Cons(T) fordítása. Márpedig Gödel második nemteljességi tétele azt állítja, hogy nem létezik, Cons(T)-nek bizonyítása, így p fordítása sem lehet az, ami ellentmondás. De az aritmetikát minden megalapozási célra szánt matematikai elméletnek tartalmaznia kell, így ellentmondásmentességének bizonyítását eszerint nem lehet semmilyen azonos erősségű metaelmélet alapján bebizonyítani. Speciálisan: az aritmetika ellentmondásmentességét nem lehet aritmetikai eszközökkel bizonyítani - ahogy azt Hilbert szándékozott volna. (Megjegyezzük, hogy az aritmetika ellentmondásmentességére transzfinit bizonyítást azonban már talált Gerhard Gentzen 1936-ban.)
A Gödel-tételek eredményeként a matematika alapjai kérdésköre kikerült a matematikafilozófia centrális problémái közül. A tételek zavarbaejtő volta miatt nehéz bármit állítani arról, hogy milyen ellentmondásmentes formális elmélet felel meg a teljes matematikának. A Hilbert által életrehívott metamatematika, mely a formális matematikai elméletek elmélete lenne matematikai eredményeit illetően beleolvadt a logikába, illetve filozófiai funkciójától teljesen megfosztva célját vesztette. Úgy tűnik, hogy a metamatikusok lemondtak arról a romantikus álmukról, hogy saját tudományuk filozófiáját minden "bölcsészeti pontatlanságtól mentesen" saját maguk, matematikai módszerekkel alkossák meg. A matematikafilozófiának azonban a russelli hagyományt követő analitikkus filozófiában kitüntetett szerepe van, minthogy szigorú tudományos nyelvezete miatt nyelvfilozófiai eszközökkel hatékonyan vizsgálható.
Matematikai realizmus vagy platonizmus
Platón ideatana
A platóni ideatan az immateriális, örök és változatlan lényegek, az ideák birodalmáról szól. Az ideák a valóság ősképei, valójában csak ők léteznek, a látható világ nem valóságos, csak érzéki csalódás. Platón a "vonalhasonlatban" mutatja be az ideák világának viszonyát a földi világ dolgaihoz. Eszerint a világ kétszer két területre tagolódik. A látható dolgok világa: közvetetten észlelhető és közvetlenül észlelhető. A szellem számára hozzáférhető világ: a tudomány területei, pl. a matematika, és az ideák birodalma.
Platón a nevezetes barlanghasonlatban írja le, az ideákhoz való fölemelkedést. Minden, amit szemünkkel látunk, amit érzékeinkkel tapasztalunk csak a tökéletlen árnykép, árnyékvilág. Ahogy a barlangban levő fényforrás a mesterséges tárgyak árnyékát a falra vetíti, valóságosnak tartják a bent élő emberek, ugyanúgy látjuk mi a világ dolgait. Világunk csak tökéletlen mása a valódi létezők, az ideák világának. Még inkább így van ez a matematikai objektumokkal. A homokba rajzolt háromszög csak földi mása "a háromszögnek".
Matematikai realizmus vagy platonizmus
A matematikára jellemző egyfajta sajátos, nagyfokú objektivitás. Akár ki is tesz két kavics mellé még kettőt, akkor négy kavcsot fog kapni. Bármelyik matematikus is végezzen el egy számítást, ugyanazon feltételek esetén, ugyanazon szabályok betartásával ugyanazt az eredményt fogja kapni. Ha mégsem, akkor egy idő után kiderül, hogy hibázott, vagy mégsem teljesen ugyanazokat a szabályokat alkalmazta.
Ez a nagyfokú objektivitás és a természettudományokban és a mindennapi életben történő egyedülálló hatékonyság a matematikusok nagy része számára egyértelmű jele annak, hogy a matematikai objektumok tőlünk független létező dolgok; bár nem fizikai tárgyakként, de objektív létezőként világunk részei. Ezt az ontológiai állásfoglalást nevezhetjük matematikai realizmusnak (más tudományok esetén, például a fizika, vagy az etika esetén szintén beszélhetünk realizmusról) illetve (kifejezetten a matematikára vonatkoztatva) platonizmusnak.
Figyeljünk föl arra, hogy a realizmus fő problematikája nem az, hogy a matematikai objektumok hol vannak. Nyilvánvaló ugyanis, hogy például a szabadsághoz való jog, a Magyar Köztársaság Alkotmánybírósága, vagy Süsü a sárkány objektív módon létezik, tulajdonságaik, viselkedésük vizsgálhatóak, elemezhetőek. (Az, hogy Süsünek hány feje van teljesen egyértelmű, objektív tény.) A platonizmus alapfeltevése, hogy a matematikai objektumokra vonatkozó állítások igaz és hamis volta tőlünk függetlenül meghatározott. Minden kijelentés vagy igaz, vagy hamis, legfeljebb ez az igazságérték az ember számára nem elérhető. A platonizmus számára a kétértékűség elve evidencia. A platonsita szemlélete tehát az, hogy a matematikai igazságokat feltárjuk, megállapítjuk, felfedezzük mintsem feltaláljuk vagy megalkotjuk.
Frege platonizmusa
Gottlob Frege az első "hivatásos" matematikafilozófus határozottan platonista volt, mint ahogy az a következő idézetből is kitűnik:
- "A botanikus éppúgy valami ténylegeset kíván megállapítani, amikor egy virág sziromleveleinak számát adja meg, mint amikor a színét. Az egyik éppoly kevéssé függ a mi önkényünktől, mint a másik. Fennáll bizonyos hasonlóság a számosság és a szín között; de ez nem abban van, hogy mindkettő érzékileg észelhető külső tárgyakon, hanem hogy mindkettő objektív.
- Azt, hogy objektív megkülönböztetem attól, hogy kézzelfogható, térbeli, valóságos. A Föld tengelye, a Naprendszer tömegközéppontja objektív, de nem szívesen nevezném valóságosnak. Az Egyenlítőt gyakran nevezzük elgondolt vonalnak; de hamis volna kigondolt vonalnak nevezni; nem gondolkodás által keletkezett, nem lelki folyamat eredménye, hanem csupán arról van szó, hogy gondolkodás által ismerjük fel, ragadjuk meg. Ha az ismerté válás keletkezés volna, akkor semmi pozitívat nem jelenthetnénk ki róla arra az időre vonatkozólag, amely megelőzi ezt az állítólagos keletkezést."
- G. Frege, Az aritmetika alapjai
A logika, az aritmetika és az euklideszi geometria tételeit ugyanúgy természettörvényeknek gondolta, mint a fizika törvényeit.
Gödel platonizmusa
Kurt Gödel saját tételeinek következményei hatására vált platonistává, eredményeit úgy interpretálta aminek szükségszerű következménye a platonizmus elfogadása lett. (Tegyük hozzá, hogy Gödel elismeréssel viseltetett azok iránt, akik kiegészítették illetve élesítették tételeit. Nagy jelentősséget tulajdonított annak az átfogalmazásnak, miszerint ellentmondásmentes aritmetikában van olyan diofantikus egyenlet, mely nem megoldható, azaz nincs olyan véges eljárás, mely megkeresné a megoldásait.)
Gödel élesen kettéválasztja a valódi vagy objektív matematika fogalmát és a szubjektív matematika fogalmát. Szubjektív matematika alatt olyan elméletet kell érteni, amely valamely formális rendszer keretein belül rekonstruálja az összes eddig ismert matematikai állítást (ilyen például egyesek szerint a halmazelmélet), melyel szemben a valódi értelemben vett matematika határait nem korlátozzák az ember által létrehozott sáncok. Gödel álláspontja szerint a valódi matematika gazdagságát nem érheti föl az emberi ész, de fontos hozzátennünk, hogy ezen kijelentését egyáltalán nem valami szentimentális közhelyként teszi, hanem tételei következményeként vezeti le. A valódi matematikára jellemző egyfajta kimeríthetetlenség, melyhez a következő két pont alapján juthatunk el.
1. Ha a szubjektív matematika axiómáit valamely véges módszerrel generálni tudnánk, akkor sem állíthatjuk, hogy ismerjük a matematikát, mert ekkor a rendszer ellentmondásmenteségét kifejező állítás nem lesz levezethető (amenyiben az egyáltalán ellentmondásmentes).
2. Hasonlóképpen, a valódi matematika is kimeríthetetlen, mert bár a konzisztenciaállítás igaz, de nem levezethető, így az emberi elme számára fel nem tárható (Gödel nyilvánvalónak tekinti, hogy a valódi értelemben vett matematika ellentmondásmentes, hiszen megvalósul).
Ez azt jelenti, hogy ha a matematika emberi alkotás lenne, akkor ismernünk kellene minden tulajdonságát, ami koránt sincs így. Ha ugyanis bár, mi teremtettük volna, de nem ismernénk pontosan működését, az csak úgy lehet, ha működése közben olyan jelenségek is fellépnek, amiket nem vettünk számításba. Ezek szintén valami tőlünk független befolyás lenne, ami így módon szintén nem általunk alkotott létezők realitását, azaz a platonizmust igazolja.
A platonista álláspont a nemteljességi tételek fényében megengedi, hogy olyan állítások is igazak legyenek, melyeket nem tudunk bizonyítani (és cáfolni sem). Amennyiben az igazságértékek metafizikai meghatározottságal bírnak, akkor az emberi elme képes lehet ezeknek az igazságoknak a felismerésére az intuíció révén. Gödel elképzelhetőnek tartja, hogy a távoli jövőben az ilyen állítások igazságát egyfajta nem matematikai indukcióval ismerhessék fel a matematikusok (ahogy az például a fizikában megszokott).
(Megjegyezzük, hogy a platonizmus védelmében és a formalizmus ellenében vetik fel azt az érvet, hogy a Fermat-sejtést évszázadokon át nem tudták korrektül bizonyítani, holott annak igaz volta minden matematikus számára, intuitív szinten teljesen bizonyosnak tűnt.)
H. Putnam: realizmus, ami nem platonizmus
Putnam szerint lehet úgy a matematika állításainak előre meghatározott értékét biztosítani, hogy közben nem kell feltennünk a matematikai tárgyak létezését. Putnam ezt a lehetséges világok szemantikájának, a modális logika szemantikájának gondolata alapján állítja. Gödel teljességi tétele értelmében ugyanis egy T elsőrendű elmélet akkor és csak akkor ellentmondásmentes, ha van modellje. Ha tekintjük a T elmélettől kissé eltérő (kissé különböző axiomatizálású) elméletek összes lehetséges modellejeinek összességét, akkor T modellje ebben egy olyan lehetséges világ, melyben T axiómái igazak. Természetesen mindannyian óhajtjuk, hogy a matematika (gödeli értelmbe vett valódi matematika) ellentmondásmentes legyen, így legyen modellje. Ez azt jelent, hogy axiómarendszere valamely lehetséges világban igaz, azaz a matematika tételei lehetséges igazságok, a matematika objektumai pedig modális egzisztenciával bírnak. Putnam állítása szerint tehát a matematika a lehetőségek és lehetetlenségek tudománya, azt mondja meg, mely állítások lehetségesek és melyek nem. Ez nagyfokú objektivitást és az igazságértékek terén teljes meghatározottságot biztosít a matematikai tételeknek, mindamellett nem kell feltételeznünk semmilyen valós létezést.
Formalizmus
A történeti formalizmus erős formája a Gödel tételek következményeként meglehetősen nagy veszteséget szenvedett. Mind Russell, mind Hilbert formalizmusa súlyos ideológiai képekkel terhelt elméletek voltak. Russell formalizmusának hátterében a logicista filozófia, Hilbertében a finitizmus állt. Mindkettőjük hitt azonban a matematika végső alapokra helyezésében, azaz egy olyan formális szuperelmélet létében, melyben az egész matematika formalizálható. (Ezt Russell a Principa Mathematica logikai rendszerében szándékozott megtenni, Hilbert pedig a finit aritmetikában). A legdestruktívabb csapást Gödel tételei az ezekhez hasonló, fundamentalista-formalista elméletekre mérte, bebizonyítva, hogy egy ilyen formális matematikai szuperelmélet ellentmondásmentességét sohasem leszünk képesek igazolni.
Ami Gödel után a formalizmusból maradt, az a modellelmélet gondolatköre. Ez a mindenféle logikákkal és ideológiákkal szemben rendkívüli toleranciával viseltető álláspont a matematikát sok formális axiomatikus elmélet együtteseként képzeli el, melyeket nem vezet vissza egyetlen elméletre. Egy matematikai elmélet létjogosultságát az biztosítja, ha formalizálható. Ez teszi egzaktá az adott részterület megállapításait. A halmazelméletnek sincs kitüntetett szerepe, pusztán segít megfogalmazni a matematikai részterületek állításait és nagy hasznát vehetjük a formalizált elméletek axiómáinak logikai vizsgálatánál. Szemben a halmazelméleti realistákkal (például a Bourbaki-csoport véleményével) a formalizmus egyáltalán nem tekinti a halmazelméleti függvényeket az analízis függvényeinek, vagy az euklideszi teret R3-nak (a valós számhármasok lineáris terének). Ezek csak halmazelméleti modelljei a megfelelő formális fogalmaknak. A formalizmus alapeszméje, hogy a matematika struktúrák összessége, melyek vagy önállóan állják meg a helyüket (értsd: végesen vagy rekurzívan axiomatizálhatóak egy formális elmélet keretében), vagy a halmazelmélet illetve a kategóriaelmélet egy elmélettöredékének minősülnek. Lényegében még az sem szükséges követelmény, hogy egy elmélet axiomatizálását kivitelezzük, elegendő, ha igazolható az axiomatizálhatóság ténye.
Ez a teljesen ideológia és teleológia mentes, a megalapozási kérdésekkel nem foglalkozó formalista hozzáállás napjaink legtöbb matematikusának matematikafilozófiai alapállása.
A kortárs formalizmus megtartotta Russell azon álláspontját, hogy a matematikai állítások nem jelentenek semmit. Ugyan van kapcsolatuk a fizikai világgal, de alapvetően olyan absztrakt kijelentések, melyek legfeljebb önmagukban hordozhatják jelentésüket. A jelentésre azonban egy formalistának amúgy sincs szüksége, mert egy tétel igazságát a formális levezetéséből nyeri és nem a jelentéséhez való viszonyából. Valójában a modern formalizmus nem filozófiai álláspont, hanem egy filozófiatagadó hozzáállás, mely által a matematikusok eltávolodhatnak a nyelvfilozófia ingoványos területétől.
A formalizmus modellelméleti kapcsolata elvezet egy másik, mai matematikafilozófiai elmélethez a strukturalizmushoz.
Strukturalizmus
A strukuralizmus nem kisebb kérdés megválaszolására vállalkozik, mint arra, hogy mi a matematika. A strukturalisták szerint a matematika a stuktúrák, minták, mitázatok elmélte. Ez a gondolat a geometria algebrizálása Klein-féle programjának, az erlangeni programnak kiterjesztése a matematika egészére. Felvethető ugyanis a kérdés, hogy a régen számok, geometriai alakzatok és végtelen kis és nagy mennyiségek tudományaként aposztrofált matematikát mi tartja össze, mitől lesz egységes tudomány a diszkréttől a folytonosig, a láttathatótól a szinte elképzelhetetlenig terjeszkedő matematikai ismeretanyag. A strukturalisták rámutatnak, hogy a matematika összes területén algebrai, relációs és topologikus struktúrákat találunk, és ezek az újra és újra előbukkanó ismerős szerkezetek (csoportok, relációk, topologikus entitások) egyáltalán nem jelentkezhetnek véletlenül. Adódnak azonban makacs fogalmak, például a természetes számok, melyek ellenállnak a struktúraként történő jellemzés kíséreltének. Sikerült azonban a kategóriaelméletben modellezni a természtes számokat, a természetesszám-objektumokat, így bebizonyosodott, hogy a számok is lényegében matematikai struktúrák.
Bourbaki halmazelméleti realizmusa
A Bourbaki-csoport fogalmazta meg először azt, hogy a struktúráknak alapvető szerepe van a matematika egységes szemlélete szempontjából. Mindezt szigorúan a halmazelmélet fogalmaival definiált struktúrákra értették és ragaszkodtak ahhoz a látásmódhoz, hogy:
- a matematika egyenlő a halmazelmélettel.
Ezzel ugyan a strukturalizmus előfutáraivá váltak, de Gödel tételeivel szembeni ellenállásuk kiszorította őket a progresszív irányzatok közül. A burbakisták Gödel eredményeit figyelemreméltó, de a matematika halmazelméleti megalapozását nem érintő kijelentéseknek minősítették. Mivel Bourbaki szerint minden matematikai entitás halmazelméleti, ezért Gödel bizonyítása is csak a halmazelméletben jön létre, így csak a halmazelméletben modellezett halmazelméletről állíthat bármit is. Ez szerintük egyáltalán nem zárja ki azt, hogy valaha, külső (pl. finit) módszerekkel igazolhassuk a halmazelmélet ellentmondásmentességét. Bourbaki véleménye filozófiai szempontból vitatható, de a matematika szemszögéből senki sem tagadhatja meg tőlük, hogy a matematikára nem másra, mint a halmazelméletre gondoljanak.
Kategóriaelméleti strukturalizmus
A strukturalizmus tekithető a formalizmus felől is. A formalizmus modern filozófiailag elkötelezetlen gondolata összefér azzal az elképzeléssel, hogy a matematika a struktúrák elmélete. Ebből a szemszögből a halmazelméletnél jobb kiindulópontot nyújt a kategóriaelmélet, melyet pont az algebrai struktúrák összességének külső vizsgálatára hoztak létre. A kategóriaelmélet a strukturalizmusban ugyanazt a szerepet tölti be, mint a formalizmusban a halmazelmélet. Ezért is dolgozták ki (egyfajta alternatív megalapozási elméletként) a kategóriaelméletre épülő logikát.
Verifikacionizmus
A verifikacionizmus a történeti intuicionizmus, elsősorban Dummett és Prawitz-féle újraértelmezése, a klasszikus logikával kapcsolatban toleránsabb formában. Nem a kizárt harmadik törvényének elvetésére teszi a hangsúlyt, hanem arra, hogy a matematikai tételek jelentését (és egyfajta episztemikus igazságát) a bizonyításunk határozza meg. A verifikacionista álláspont tehát szorosan kapcsolódik a formalizmushoz, amennnyiben a formális bizonyításokat tekinti az érvényesség egyetlen feltételének, de a formalizmussal szemben metafizikai tartalmat is hordoz, amennyiben tagadja az igazságértékek valós létét. Eszerint az álláspont szerint az állítások három kategóriába sorolhatók: -bizonyíthatók, -cáfolhatók és -kontingensek (se ez, se az). |

